Continued from IMAGE TEST PATTERN 1.
My first take for this one was almost exactly the same as my one for IMAGE TEST PATTERN 1, except that the pixel plotting loop alternates between white (3) and black (0) for the checkerboard pattern instead of just drawing solid white:
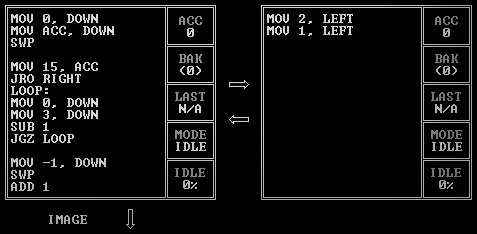
The tricky bit in this is the JRO RIGHT that reads in 2 for even rows (starting counting at zero) and 1 for odd rows. JRO 1 is effectively a NOP, so for odd rows nothing happens and it draws black, white, black, etc. However, for even rows, it’ll skip the MOV 0, DOWN the first time and draw white, black, white, etc. This means that it’ll only draw twenty-nine pixels in even rows, but luckily the thirtieth pixel in even rows starts off as black and we want it to be black, so it’s okay to skip it.
This runs in 1,794 cycles, which is better than the original IMAGE TEST PATTERN 1 solution it’s based on because the loop is already partially unrolled: it draws two pixels per pass instead of one because the two have different colors.
Just like the first problem, we can improve on this by unrolling the loop more and replacing the column counter with another unit:
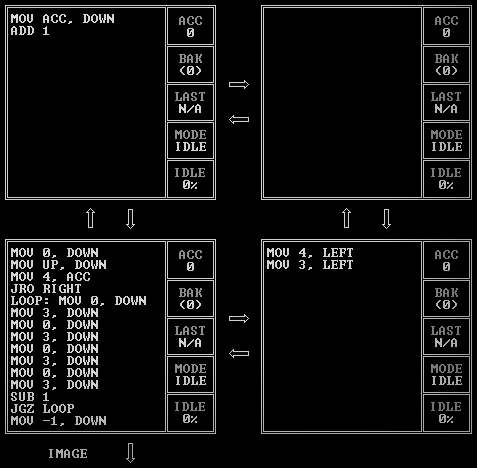
This is essentially the same as the final code for IMAGE TEST PATTERN 1 with two differences: the loop prints out 0 and 3 instead of just 3, and the JMP into the middle of the loop is replaced with the JRO RIGHT into the middle of the loop to handle starting alternate rows with different colors.
This runs in 1,346 cycles, which is faster than IMAGE TEST PATTERN 1’s final score of 1,364. How is that possible? I said the answer a few paragraphs ago: we only draw twenty-nine pixels in even rows! Drawing a pixel takes two cycles, one for the unit to send the color value down and one for it to be read, so for the nine even rows we save eighteen cycles, which is exactly the difference between 1,364 and 1,346.
Which begs the question: why can’t we draw twenty-nine pixels in odd rows too? Let’s take a different approach: for every row we’ll draw the same twenty-nine pixel slab of [3, 0, 3, 0, …, 3], but in even rows we’ll start drawing in the first column and in odd rows we’ll start drawing in the second:
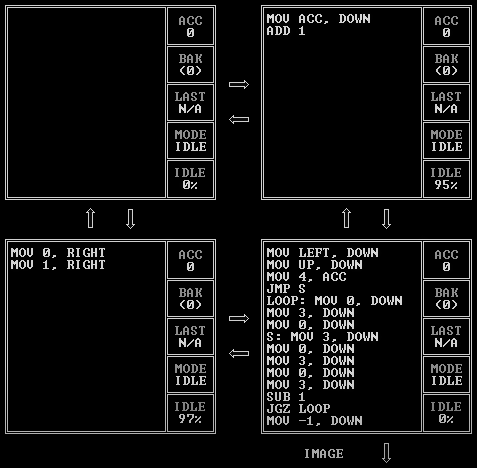
The initial MOV 0, DOWN has been replaced with another read from another unit that tells it which column to start drawing in. This unfortunately adds a one cycle penalty to this solution, because the drawing unit’s first instruction is to read from that unit and it’ll take one cycle for it to provide its first value. If I could fit more code into the drawing unit, I could have it send a hardcoded 0 down for the very first row and have it read from left for every row after that to reclaim that lost cycle.
Because we’re now always drawing twenty-nine pixels per row, we can replace that JRO RIGHT trick with just a plain JMP and eliminate that unit on the right that provided its offsets.
Removing a pixel from another nine rows saves us another eighteen cycles, bringing us down to our final result of 1,346 – 18 + 1 = 1,329.